From geometry to dynamics: Learning overdamped Langevin dynamics from sparse observations with geometric constraints

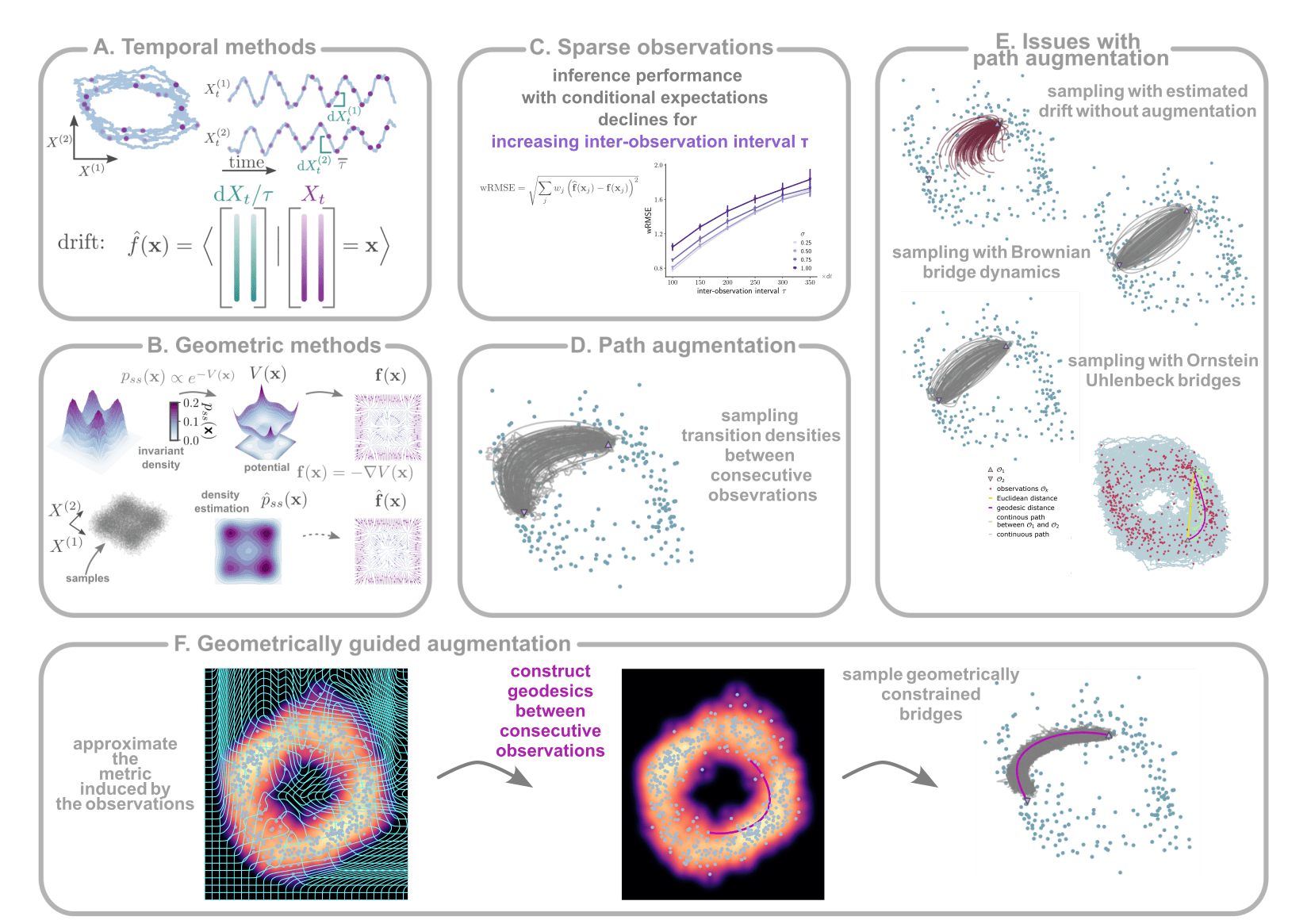
We proposed a method for introducing geometric inductive biases into the inference of stochastic systems.
The central idea is to view the deterministic flow field as a scaffold upon which system states fluctuate, and to approximate this scaffold in terms of distortions of a metric induced by the observations.
This effectively approximates the low-dimensional invariant density (empirical manifold) without the need to project to a lower dimensional space (whose dimensionality would be hard to estimate due to the presence of fluctuations).
The central premise then is that geodesics computed on the empirical manifold wrt the approximated metric consitute the most probable path between consecutive observations in the Onsager-Machlup sense.
We employed this most probable path as a control constraint to perform path augmentation between consecutive observations, and employed these estimated latent paths for inference of th eunderlying flow field.

See here the preprint

This project has been presented as a talk at:

• TUM during my interview talk at the Gjorgjieva lab - April 2023 (together with the the work on inference of synaptic connectivity under the name “Geometric methods for inference”)
• Flatiron institute - April 2024 (together with the work on inference of latent neural dynamics)
• Institute for Adaptive and Neural Computation, University of Edinburgh - May 2024 (together with the work on inference of latent neural dynamics)

and as a poster at:

• NeurIPS 2022 - Machine learning for the physical sciences workshop (see related short paper)
• Recent advances in understanding Artificial and Biological Neural Networks, École de physique des Houches, Les Houghes, Feb. 2023
• ICLR 2023 - Physics for machine learning workshop (see related short paper)